TABLE OF CONTENTS

• Introduction
• Some facts about the used schedule
• Challenge
• Jumping straight into the results
• Definitions and Calculations

---

Introduction

One of the main challenges with transferring data from Safran to P6 is the simple fact that Safran can have assigned calendars for each individual link, whereas P6 cannot (it typically has a setting that makes it use either the predecessor or successor activity's calendar). 

The only "self defense" against this architectural incongruency is to adjust the lags in accordance with the calendar "differences", so that the end result (early dates) will become the same in source and destination.

This article will outline how this is achieved and the effects it has on a simple example schedule with some well defined activity calendars and link calendars (where each link has lag <> 0):

Some facts about the used schedule

The test schedule (Safran) used for benchmarking the effects of "lag adjustments" in P6 download.

Each of the (non-milestone) activities have a duration of 10 days, and each link has a lag of 10 days. Activities use these calendars, in order from top to bottom: 2_5, 4_5, 6_5, and 8_5 (*)

Each of the links have these individual calendars, in order from top to bottom: 3_5, 5_5, and 7_5 (*)

(*) Example:  2_5 means 2 hours per day for 5 days a week)

Challenge

How can the P6 schedule engine get the "same" result (i.e early start and finish dates) when it uses Successor Activity’s calendar for lag (and similarly for using the Predecessor’s calendar)

The goal is to show how the lags, when downloading the schedule into P6, can be adjusted so that the end result of schedule engine will be as close to the original Safran schedule as possible. 

Option in HSP for Config or IEA.

Jumping straight into the results

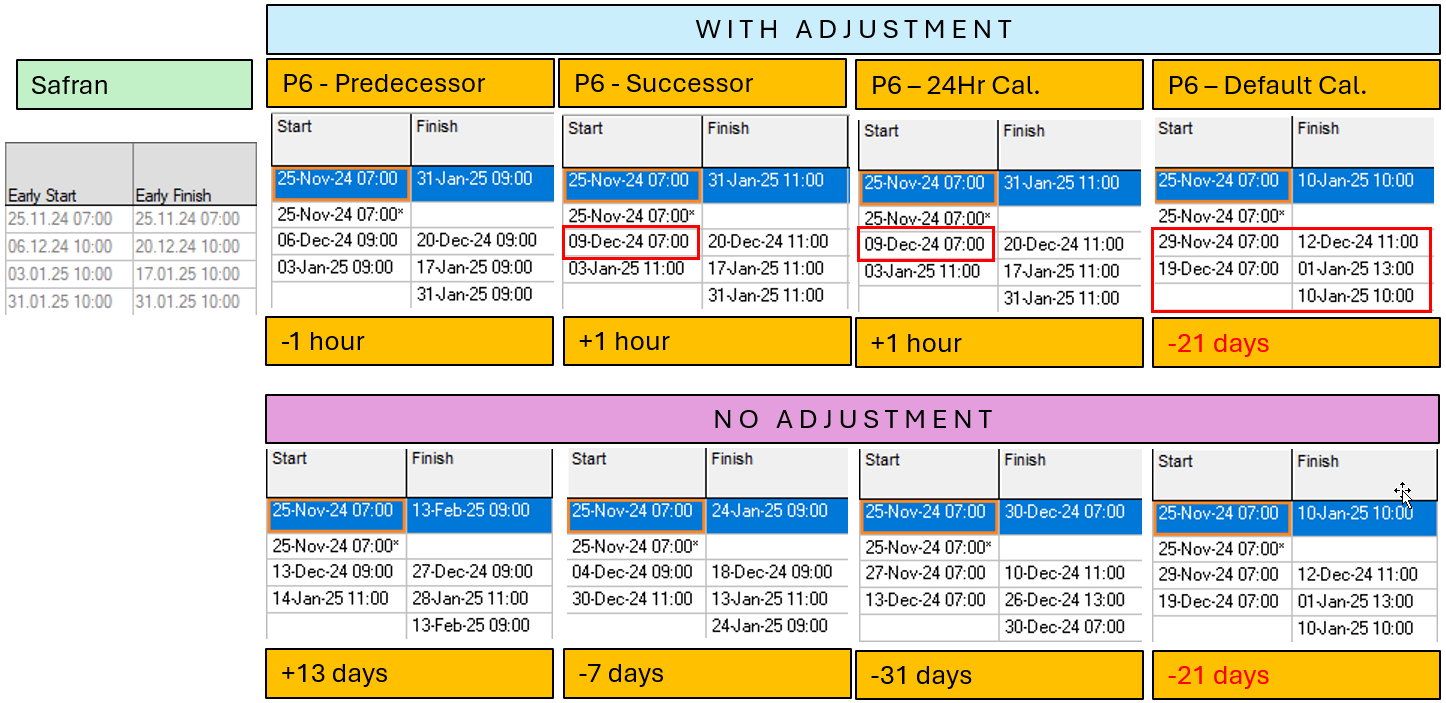
The un-adjusted result was empirically found to be either +13 days of project duration, or -7 days, depending on the P6 option set (first 2 options, respectively):

The setting in P6 that is read by IDE to optionally automatically adjust links (see matrix below).

And the adjusted result was empirically found to be -1 hour and +1 hours respectively.

Below is the matrix showing empirical result for each of the 4 options (seen above). 

NOTE: For the 4th alternative, there is no effect of changing lags, and it seems to be a bug in P6 as the result will not change even if the default calendar and lags are changed. 

Matrix showing the empirical result of "lag adjustment" for each of the 4 P6 schedule options.

 

Definitions and Calculations

Let's create a term called "Weekly workhours for a calendar" and have it defined as the total weekly hours that the calendar supports. Example 8_5 (8hrs for 5 days) results in 40 weekly workhours.

Lets call this Wwh (Weekly workhours) and denote the link’s Wwh as Wwh(l) and the Wwh for activity (successor in this example) as Wwh(a)

Then the "lag factor", i.e the number to multiply the original lag with, is the ratio of these: Wwh(a) / Wwh(l)

 

Calculations (when using successor calendar)

Link 1:
Lag = 10d, Calendar is 3_5, i.e Wwh=15
Successor activity uses calendar 4_5, Wwh=20
The link factor is 20 / 15 = 1.333, i.e the adjusted lag is 10*1.333 = 13.33d

Link 2:
Lag = 10d, Calendar is 5_5, i.e Wwh=25
Successor activity uses calendar 6_5, Wwh=30
The link factor is 30 / 25 = 1.2, i.e the adjusted lag is 10*1.2 = 12d

Link 3:
Lag = 10d, Calendar is 7_5, i.e Wwh=35
Successor activity uses calendar 8_5, Wwh=40
The link factor is 40 / 35 = 1.143, i.e the adjusted lag is 10*1.143 = 11.43d

Given these adjustments the difference is empirically reduced in P6 from -7 days to about +1 hours deviation.

 

Calculations (when using predecessor calendar)

Link 1:
Lag = 10d, Calendar is 3_5, i.e Wwh=15
Predecessor activity uses calendar 2_5, Wwh=10
The link factor is 10 / 15 = 0.666, i.e the adjusted lag is 10*0,666 = 6.66d

Link 2:
Lag = 10d, Calendar is 5_5, i.e Wwh=25
Predecessor activity uses calendar 4_5, Wwh=20
The link factor is 20 / 25 = 0.8, i.e the adjusted lag is 10*0.8 = 8d

Link 3:
Lag = 10d, Calendar is 7_5, i.e Wwh=35
Predecessor activity uses calendar 6_5, Wwh=30
The link factor is 30 / 35 = 0.857, i.e the adjusted lag is 10*0.857 = 8.57d

 

Given these adjustments the difference is empirically reduced in P6 from +13 days to -1 hour deviation.